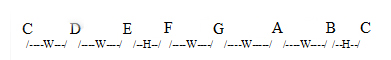Basic theory knowledge
What follows is just a brief summary of basic theory and harmony necessary to understand practical applications on your instrument.
The natural sounds are:
C – D – E – F – G – A – B
You might also find in some books the name of these notes in Italian (nothing to do with ‘solfege’!)
Do, Re, Mi, Fa, Sol, La, Si and in German C, D, E, F, G, A, H.
Sharps and flats.
# = sharp: raises the given note of a half step.
## = double sharp: raises the given note of two half steps (also noted ‘x’).
b = flat: lowers the given note of a half step.
bb = double flat: lowers the given note of two half steps.
= natural: cancels sharps and flats (double natural cancels double sharps and flats).
The Chromatic scale.
The chromatic scale contains all 12 natural and altered sound (using sharps and flats).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | C#/Db | D | D#/Eb | E | F | F#/Gb | G | G#/Ab | A | A#/Bb | B |
Notes called with a different name, but identifying the same sound, are called enharmonic (i.e.: C# e Db). The shortest distance between two sound of the chromatic scale is a Half Step, the distance of a fret on the guitar.
Intervals.
An interval is the distance between two notes.
Intervals of a second, third, sixths and seventh are called major. If a major interval is raised by an half step it is called augmented. If a major interval is lowered by an half step it is called minor. If lowered by two half steps, diminished.
Intervals of a fourth, fifth and octave are called perfect. If a perfect interval is raised by an half step it is calledaugmented. If a perfect interval is lowered by an half step it is called diminished (note the difference).
All the intervals from the tonic of a major scale to any other note of tha scale are major or perfect (i.e. between C and D=major 2nd, C e E=major 3rd, C e F=perfect 4th, and so on…)
Intervals can also be calculated summing up half steps:
|
N.of htps |
1 | 2 | 3 | 4 | 5 | 6 | 6 | 7 | 8 | 8 | 9 | 10 | 10 | 11 | 12 |
| Interval | m2 | M2 |
m3 |
M3 |
P4 |
4aug |
5dim |
P5 |
5aug |
m6 |
M6 |
6aug |
m7 |
M7 |
P8 |
where m=minor, M=major, P=perfect, dim=diminished, aug=augmented.
How to build a major scale.
The spacing of the notes in a major scales follow this rule:
WWHWWWH
Where W = Whole step (a major second) H= Half step (a minor second)
Example : C major
To build major sales in other keys use exclusively either sharps or flats choosing the notes so that a note with the same name is never repeated. In doing so you will only use Diatonic half steps (given by two notes with different name, i.e. C-Db, opposite to Chromatic half steps given by two notes with the same name, as in D –D#).
This is a list of all the major scales in all keys. The order follows the amount of sharps and flats in the key.
Keys with flats.
| C | D | E | F | G | A | B |
| F |
G |
A |
Bb |
C |
D |
E |
| Bb |
C |
D |
Eb |
F |
G |
A |
| Eb | F | G |
Ab |
Bb |
C |
D |
|
Ab |
Bb |
C |
Db | Eb |
F |
G |
|
Db |
Eb | F |
Gb |
Ab |
Bb |
C |
|
Gb |
Ab |
Bb |
Cb |
Db |
Eb |
F |
|
Cb |
Db |
Eb |
Fb |
Gb |
Ab | Bb |
Keys with sharps.
| C | D | E | F | G | A | B |
|
G |
A | B | C | D | E | F# |
|
D |
E | F# | G | A | B | C# |
|
A |
B | C# | D | E | F# | G# |
| E | F# | G# | A | B | C# | D# |
| B | C# | D# | E | F# | G# | A# |
| F# | G# |
A# |
B | C# | D# | E# |
| C# | D# | E# | F# | G# |
A# |
B# |
Relative minor (key)
Every major key has one relative minor which is made of the same notes, but starting from the sixth note. In other words, starting a minor third below (or a major sixth above) the root of the major scale. For example if we take C major its relative minor is A minor, spelled A B C D E F G.
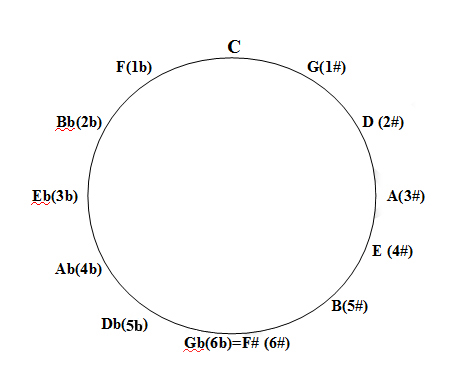
Circle of fifths.
The circle of fifths one of the most used ways to summarize all I explained so far. It is very useful to memorize how many and which alterations a specific key has.
I find very useful to memorize FCGDAEB and the same sequence backwards BEADGCF. The first is the order of sharps the second, of flats. So if a key has, for example, 3 sharps (A major) they will be the first 3 notes in the first seqence (F# C# G#).
Harmonized major scale – How to build chords.
In the example below every note of a major scale identifies a ‘degree’ of the scale. In the example I have used C major, but this is valid for every other major scale in any key.

If I stack on every degree two more notes a diatonic third apart (basically every other one) I end up with different kinds of triads (triad=group of three notes). These triads are shown in the example below. If we analyse the intervals between notes:
a Major Triad has a Maj 3rd and a Perf 5th (Eg. C-E-G: C-E=maj 3rd , C-G Perf 5th).
a Minor Triad has a min 3rd and a Perf 5th.
a Diminished Triad has a min 3rd and a diminished 5th.
You will have the same series of chords in all the other keys Eg: F major: F, Gm, Am, Bb, C, Dm, Em.
If we stack another note a diatonic third apart from the last note of the above triads we will have Seventh chords.
This again is valid for all the 12 keys. This concept is vital to understand how songs are built and how to pick the correct scale for a solo.
The above concept in all keys looks like this:
Harmonized major scale – Keys with flats.
|
Cmaj7 |
Dm7 |
Em7 |
Fmaj7 |
G7 |
Am7 |
Bm7b5 |
|
Fmaj7 |
Gm7 |
Am7 |
Bbmaj7 |
C7 |
Dm7 |
Em7b5 |
|
Bbmaj7 |
Cm7 |
Dm7 |
Ebmaj7 |
F7 |
Gm7 |
Am7b5 |
|
Ebmaj7 |
Fm7 |
Gm7 |
Abmaj7 |
Bb7 |
Cm7 |
Dm7b5 |
|
Abmaj7 |
Bbm7 |
Cm7 |
Dbmaj7 |
Eb7 |
Fm7 |
Gm7b5 |
|
Dbmaj7 |
Ebm7 |
Fm7 |
Gbmaj7 |
Ab7 |
Bbm7 |
Cm7b5 |
|
Gbmaj7 |
Abm7 |
Bbm7 |
Cbmaj7 |
Db7 |
Ebm7 |
Fm7b5 |
|
Cbmaj7 |
Dbm7 |
Ebm7 |
Fbmaj7 |
Gb7 |
Abm7 |
Bbm7b5 |
Harmonized major scale – Keys with sharps.
|
Cmaj7 |
Dm7 |
Em7 |
Fmaj7 |
G7 |
Am7 |
Bm7b5 |
|
Gmaj7 |
Am7 |
Bm7 |
Cmaj7 |
D7 |
Em7 |
F#m7b5 |
|
Dmaj7 |
Em7 |
F#m7 |
Gmaj7 |
A7 |
Bm7 |
C#m7b5 |
|
Amaj7 |
Bm7 |
C#m7 |
Dmaj7 |
E7 |
F#m7 |
G#m7b5 |
|
Emaj7 |
F#m7 |
G#m7 |
Amaj7 |
B7 |
C#m7 |
D#m7b5 |
|
Bmaj7 |
C#m7 |
D#m7 |
Emaj7 |
F#7 |
G#m7 |
A#m7b5 |
|
F#maj7 |
G#m7 |
A#m7 |
Bmaj7 |
C#7 |
D#m7 |
E#m7b5 |
|
C#maj7 |
D#m7 |
E#m7 |
F#maj7 |
G#7 |
A#m7 |
B#m7b5 |
In a simple chord progression/ tune things should now be easy to analyze:
| C7 | … the V7 of F major, the key is F major.
| Cm7 F7 | Bbmaj7 | … a ii – V – I in Bb major. The Key is Bb major.
| A maj7 F#m7 Bm7 E7 | … a I-vi-ii-V in A
Of course this is simple when the tune is all in one key, it becomes a skill to be able to spot these in a tune that features key changes and other compositional tricks. This is beyond the scope of this lesson.
Hope this helped!